 tm
tmThe MULTIDIMENSIONALITY of ZigZag® tm
As we said back at "The Connections
of ZigZag", we all have had some everyday experiences of connection-space--
but we haven't really thought of it as a space.
For instance, an ordinary list, on paper, is a connnective structure in one dimension-- a one-dimensional connection-space.THE GENERAL CASE of dimensionality is N.A spreadsheet, and hierarchical directories of computers, exist in two-dimensional connection-space, as follows: a checkerboard, or a spreadsheet, is a connective structure in two dimensions Those two dimensionsare called rows and columns.
Hierarchical directories are also connective structures in two dimensions.
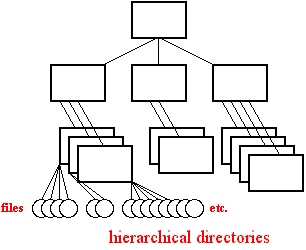
But the dimensions of hierarchical directories are called "up-down" and "contents". Which basically means that people aren't thinking of hierarchical directories as a special case of anything else.
But we are, and we hope you will too.
This means mathematicians agree that if you have more dimensions than two, there's no reason to stop at three (except tradition), and you ought to be able to have as many dimensions as you want.THE FIRST THREE DIMENSIONS IN ZIGZAGThis is true for connective dimensions just as it is true for continuous dimensions-- dimensions that have distance.*
The ZigZag system is about connective structures in as many dimensions as you like.* We are familiar with four dimensions that have distance. But every schoolkid knows that these three dimensions of space were generalized by Einstein into a fourth dimension of time. It is less well known that they are further generalized by mathematicians into such systems as Hilbert-space. Three-dimensional computer graphics actually relies on four-dimensional mathematics, and one researcher, Thomas Banchoff, actually offers software for the study of four-dimensional continuous spaces on a screen.
We are going to allow structures to exist in as many dimensions as you like.WHAT DO DIMENSIONS LOOK LIKE?We will call the first three dimensions d.1, d.2, d.3. (By convention we recommend beginning the name of a dimension with "d.".)
A dimension has a positive direction and a negative direction. For example,
Let's start by simplifying the question. What do the first three dimensions look like?USER-CREATED DIMENSIONSHere's a view of two ZigZag windows looking at the same data-- in two different dimensional views. (You may have already seen this before in "The Views of ZigZag". But we'll point out something different here.)
Each window has a little guide, in its upper left corner, telling which dimensions are being shown in that window.
In the left window, we see that the horizontal dimension is d.1 and the positive direction in d.1 is to the right. We see further that the vertical dimension is d.2, and the positive direction in d.2 is downward. A third dimension is also mapped, d.3-- assigned to the forward-and-back dimension-- that is, toward the screen from the user and vice versa. (It's not clear from the diagram, but the negative direction is forward from the user to the screen, and the positive direction of d.3 is toward the user.)
In the right-hand window, however, there is a different view: d.3 is now on the horizontal axis, with positive toward the right. (d.3 is also forward-and-away, in this illustration.)
What this overall picture shows is that the ZigZag user can see the same structure in different dimensional views at once.
We're not giving all the directions here,
but it is possible to rotate any of these axes to show any different dimension of ZZspace.
It is also possible for the user to create new dimensions at any time.What do the other dimensions look like?
Exactly the same, except for special-purpose dimensions used by the system (such as d.cursor, d.clone).
Have you read "The Axioms of ZigZag Structure" yet?
How about "The Views of ZigZag"?
Or "Special Properties of ZigZag Structure"?
Back to WELCOME TO ZIGZAG.